戥秤最早出现于宋代,是我国特有的一种计量工具,旧时专门用来称量金、银、贵重药品及香料的精密衡器。其对微量计重比起一般杆秤,达到前所未有的精密程度,是古代衡器制造史上一个重大创新。
戥秤因用途不同,可细分为金戥、银戥、药戥、珠戥等许多种类,其中有一种叫线戥(也称“分厘戥”、北方俗称“麦杆秤”)。这种秤杆极细、极长的戥秤,把戥秤的微计量特点发挥到了极致,做工在诸多戥子中也是最难的。这种戥秤在古代有一个非常奇妙的用途,可以直接称验出黄金的成色,这种方法叫“隔水称金法”。
线戥的工艺结构分析
线戥的结构同普通戥秤没有区别,但杆更加细长,砣非常小,做工更加精细,可以说是戥秤中的极品。
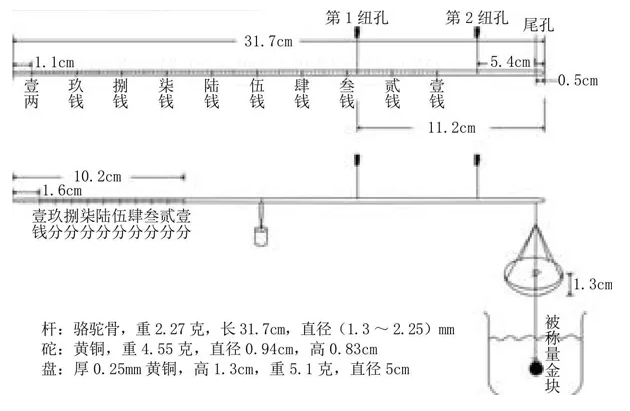
在我多年的收藏中就有几杆这样的线戥:盒为红木质地,杆为骨质。以其中之一为例:杆长度达到31.7厘米,重量为2.27克,用游标卡尺测量杆的直径,大处只有2.25毫米,小处只有1.3毫米,非常纤细,比普通牙签略大(见下图);上面是两行刻度,头纽称量范围是1钱至1两,二纽称量范围是0至1钱。盘为厚0.25毫米的黄铜质,直径5厘米,重5.1克。砣是一个直径0.94厘米、高0.83厘米的小圆柱体,经检测重量为4.55克,折合清代计量标准为1钱2分,为非定量砣。盒的铜扣件采取了非常巧妙的暗推倒钩结构,设计十分完美实用,以至于在数百年后的今天还能轻松开启。
工作原理:杠杆原理。将杆的长度做得足够长,并选用轻巧的砣,减少秤量的最大值,就可以更加细分刻度,达到提高计量准确度的目的。如上所述的秤,头纽量程细分为90等份,每格对应重量读数为1分(0.37克);二纽最大秤量值只有1钱,细分为100等份,每格对应读数为1厘(0.037克)。这样的准确度甚至超过了现代一般的电子秤。
为什么要把杆做得如此细小,原因就是尽量减少杆的自身重量对称量物品的影响。常用骆驼腿骨做杆,这种骨头的质地坚韧、轻盈、气孔少,而且足够长,是做线戥的理想材料。如此纤细的杆,非常容易折断,就是今天拿出来观察时,都需要非常小心。更何况是历经几百年,经常使用的物件,能保存如此完整,非常难得。
线戥在古代的使用
线戥在古代的常用地方有两个:当铺和钱庄。
清中后期至民国,因战乱导致民不聊生,却是当押业发展的黄金时代。据《泽国镇志》记载:“清道光年间(1821-1850),阮敬熙始营质库,至光绪二十年(1894),成为阮有泰当铺。光绪三十年,阮氏在麻车桥、黄岩石曲分别开设阮有裕、阮由义堂当铺。民国6年(1917),阮氏在前街鹤池畔开设阮有丰当铺,坊间称‘前当’,开设在下街的阮有泰当铺称‘后当’。两当铺共有资金4万元,进行存、押款业务,年营业额14万元。”各店获利甚丰,生意稳定,当铺越开越多,至“民国27年12月24日,温岭县成立典当业同业公会,泽国阮尚傅为主席委员,会员家数17家,民国33年3月解散”(《泽国镇志》第218页“当铺”)。
当押业押入的货物极为复杂,“有贵重的金银、玉器、古董字画,一般的有冬夏衣衫、棉被蚊帐、家常用具,凡当铺允许的典当物件都可以抵押兑钱。典当物品一般按当时实价三分之一定价,全新的不过五六成,金银饰品也只以市价七八成押价,书画、古物等凭眼力估价。”看货定价的“管保”(当铺的掌柜)责任最重,多是先从“柜头”(小伙计)做起,既靠实践,亦靠师承,凭的就是经验。其中鉴别、称量各种金银珠宝、玉器钻石就要用到线戥。
这几把线戥,应该就是当时当铺或钱庄所用。因当押之物多为穷人家中戒指、耳环之类小件金器,重量多在一钱左右,很少超过一两的大件,所以这种类型的戥秤最大秤量也在一两之内。其中一把秤盘盒的上面,还保留了一张写了“兑”的垫纸(见下图),意思是“兑换”“校兑”之意。秤盒上有一“甫”字,应该是店铺字号或秤的主人名字简称。
验证“隔水称金法”
黄金是贵金属,成分高低直接影响到它的价值。在古代,人们要使用黄金交易,是如何检测黄金的成色的呢?即用戥秤“隔水称金法”(见下图)。
这种方法先用线戥称出金件重量,再吊入水中称,将称得的重量互相比较,便知金的成色。据老一辈当押业掌柜积累的经验,有以下换算口诀:“足金一两,九钱五分;每降一成,重减五厘”。意思是足金一两,在水中重九钱五分;九成金一两,在水中重九钱四分五厘;八成金一两,则水秤得九钱四分;以此类推。
这里涉及的原理是阿基米德浮力定理。我们知道每一个不同的物质有不同的密度,密度越大,同样重量的体积就越小,这样在水中的浮力就越小。黄金是密度非常大的金属,达到了19.3克/立方厘米。银的比重为10.49克/立方厘米;铜的比重为8.9克/立方厘米。同体积大小的黄金重量是铜重的2.17倍,银重的1.84倍。由于浮力的作用,同样重量金放在水里称,重量减轻少,银放在水里称,重量减轻多。
下面再用数学的方法分析:假设有块合金含金450克,含银50克,为九成金。放入水中它的重量=500克-浮力。设450克金的浮力为x,50克银的浮力为y,根据浮力定理:x=450克÷19.3克/立方厘米×1克/立方厘米(水的密度)=23.3克,y=50克÷10.49克/立方厘米×1克/立方厘米(水的密度)=4.77克。由此可以得出此合金在水中的浮力=23.3克 4.77克=28.07克,在水中称得的重量=500克-28.07克=471.9克。而按照上述口诀计算,在水中称得的重量应为500克×94.5%折=472.5克。我们可以看到两者结果相差只有0.1%,可以说非常接近。
实验:取纯金戒指一枚,上秤得重量为4分8厘,折合为1.76克(按照清康熙十八年官颁标准砝码,十两重量366克计算,一分折合重为0.366克),经电子秤测量实际重量为1.72克,相差0.04克,此秤误差率为2.3%。按照上述口诀,在水中称得重量的计算列式为4分8厘×95%=4分5厘6毫。然后用细线吊戒指于水中称得重量为4分6厘,非常准确。
继续以上所述的戒指为纯金件,取纯银0.18克,合计总重为1.90克,折合金成色为1.72÷1.90=90.5%,可以认为是九成金。复用上述办法,在空气中称得重量为5分3厘,在水中称得的重量为5分整,用口诀列式为5分3厘×94.5%=5分零6毫,结果表明,完全符合实验的结果。
由此可见,古代人们总结的这种方法是非常科学,而且是行之有效的。
注:作者为浙江省级非物质文化遗产泽国颜氏戥秤第六代传人。
本文刊发于《中国计量》杂志2019年第12期 作者:浙江省温岭市城南镇政府 叶永峰
 计量资讯速递
计量资讯速递
 计量资讯速递
计量资讯速递